Entangled Coin

Description

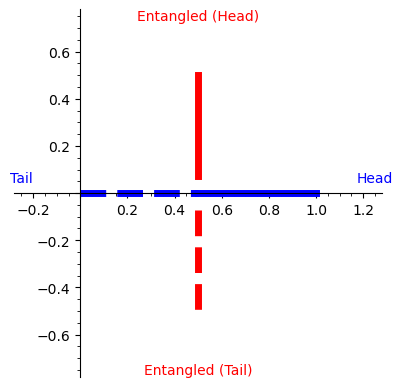
This demo simulates an "Entangled Coin" whose toss behavior depends on a user-controlled wheel. The wheel’s angle (from 0° to 360°) sets a parameter q = angle/360 that governs the coin's dynamics:

• 0 <= q <= 1/2: This is a usual Bernoulli coin with probabilities a and b = 1-a
• 1/2 < q < 1: With probability q the coin flips (yielding the complement of the last outcome), and with probability 1–q it remains the same.

In addition, we show the complex probabilities computed via the formula \[ a = \frac{1 \pm \sqrt{1-2q}}{2}, \quad b = 1-a, \] where the square root can become imaginary if \(1-2q < 0\).